An interesting equation: x/(y+z)+y/(z+x)+z/(x+y)=4 x,y,z∈Z+
1 Meeting the equation
The author have seen a problem on the Internet: Find positive integers \(x,y,z\) that satisfies equation \(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}=4\).

(Thinking this equation is easy to solve? Try it before continue reading!)
One might want to solve it by brute-forcing with a computer (for example, using Python programming language):
from fractions import Fraction as Frac n = 100 print('Solutions:') for x in range(1, n + 1): for y in range(1, n + 1): for z in range(1, n + 1): if Frac(x, y + z) + Frac(y, z + x) + Frac(z, x + y) == 4: print((x, y, z))
Solutions:
However, it does not help.
Try with Wolfram Mathematica:
FindInstance[x/(y + z) + y/(z + x) + z/(x + y) == 4, {x, y, z}, Integers]
{{x -> 11, y -> 9, z -> -5}}
It gives an integer solution, but not a positive integer solution. Adding more constraints may solve this problem:
FindInstance[x/(y + z) + y/(z + x) + z/(x + y) == 4 && x > 0 && y > 0 && z > 0, {x, y, z}, Integers]
FindInstance::nsmet: The methods available to FindInstance are insufficient to find the requested instances or prove they do not exist.
FindInstance[z/(x + y) + y/(x + z) + x/(y + z) == 4 && x > 0 && y > 0 && z > 0, {x, y, z}, Integers]
Unfortunately, it does not work either!
This equation is much harder than expected. Only experts in the field of number theory will have a chance to solve it. The smallest solution to this equation is:
x = 36875131794129999827197811565225474825492979968971970996283137471637224634055579 y = 154476802108746166441951315019919837485664325669565431700026634898253202035277999 z = 4373612677928697257861252602371390152816537558161613618621437993378423467772036 from fractions import Fraction as Frac print(Frac(x, y + z) + Frac(y, z + x) + Frac(z, x + y) == 4)
True
They are indeed enormous numbers since the most significant number has 81 digits. Surely brute-forcing would take an unacceptably long time.
(If you know some mathematics lovers, share them with this enjoyable problem!)
(Image above is from xkcd)
How to obtain this enormous solution? The answer will be given below.
2 Diophantus's problems
This equation is simple on the outside, but complicated on the inside. Equations like this have puzzled the best mathematicians in this world for thousands of years. Diophantus of Alexandria, a Hellenistic mathematician of the 3rd century, made a study of several polynomial equations of this form:
\[P(x_{1},x_{2},\dots,x_{k})=\sum _{{0\leq i_{j}\leq n_{j}}}a_{{i_{1}i_{2}\dots i_{k}}}x_{1}^{{i_{1}}}x_{2}^{{i_{2}}}\dots x_{k}^{{i_{k}}}=0\]
Equations of this type are Diophantine equations. For example, \(x^2+y^2=z^2\) (\(x,y,z\) are the unknowns) is a Diophantine equation. System of Diophantine equations can be reduced to a Diophantine equation by means of \({\displaystyle\sum_i (RHS_i-LHS_i)^2=0}\). So this article will only discuss situations that contain one equation.
After applying reducing to common denominator technique to the equation in the beginning, an equivalent equation is obtained:
\[x^3 + y^3 + z^3 - 3x^2(y+z) - 3y^2(z+x) - 3z^2(x+y) - 5xyz=0\]
This equation is indeed a Diophantine equation! More precisely, a degree-3 homogeneous Diophantine equation (all items in this equation are of degree \(3\)).
2.1 Degree-1 Diophantine equation
Degree-1 Diophantine equations are very easy to solve. There is an important lemma called generalized Bézout's lemma, which states that an equation \(a_1x_1+a_2x_2+\dots+a_nx_n=c,\quad a_i,c\in\mathbb{Z}\) has a solution if and only if \(\gcd(a_1,a_2,\dots,a_n)\mid c\). It's easy to construct all solutions of a degree-1 Diophantine equation using this lemma.
When solving \(n=2,\,c=1\) case, extended Euclidean algorithm is commonly used:
def extended_euclid(a, b): if b == 0: return 1, 0, a else: x, y, q = extended_euclid(b, a % b) x, y = y, (x - (a // b) * y) return x, y, q print(extended_euclid(47, 30))
(-7, 11, 1)
Then \((x,y)=(-7,11)\) is a solution to equation \(47x+30y=1\). It is easy to prove that all solutions to this equation are \((-7+30t,11-47t),\quad t\in\mathbb{Z}\).
2.2 Degree-2 Diophantine equation
Degree-2 Diophantine equations are harder, but still fully understood by mathematicians. A classical example is Pell's equation:
\[x^2-ny^2=1,\quad n\in\mathbb{Z}^{{}+}\]
When \(n\) is a square number, it only has trivial solutions \((x,y)=(\pm 1,0)\). But for other cases, Lagrange proved that infinitely many distinct integer solutions exist. A fundamental solution can be obtained via continued fractions, and all additional solutions can be generated recursively (using formula \((x_{i+1},y_{i+1}) = (x_1 x_i + n y_1 y_i, x_{1}y_{i}+y_{1}x_{i})\)) from the fundamental solution.
Code for finding the fundamental solution of Pell's equation (requires sympy installed):
from sympy import sqrt from fractions import Fraction as Frac def continued_fraction(n): a = sqrt(n) while True: yield (int(a)) a = 1 / (a - int(a)) def pell(n): if int(sqrt(n))**2 == n: return (1, 0) l = [] for i in continued_fraction(n): a = Frac(i) for j in l[::-1]: a = j + 1 / a if a.numerator**2 - n * a.denominator**2 == 1: return (a.numerator, a.denominator) l.append(i) print(pell(661))
(16421658242965910275055840472270471049, 638728478116949861246791167518480580)
From the result above, one can know that the fundamental solution can be huge even if \(n\) is small. However, there is a known upper bound \(x\lt n^{\sqrt n}\) for large enough \(n\).
2.3 Degree-3 Diophantine equation
Above texts showed that the equation in the beginning is a degree-3 Diophantine equation. Equations of this kind are very hard, related to very deep theories and numerous open problems.
However, fortunately, this equation is relatively easier to solve, since it is homogeneous and has only \(3\) variables. One can quickly transform it into an elliptic curve, which has many beautiful algebraic properties. Using properties of elliptic curves, one can generate infinitely many solutions (which may not be positive) from a non-positive solution and finally find a positive solution.
3 Transforming to elliptic curve
Since the equation is homogeneous, if \((x_0,y_0,z_0)\) is a solution, \((kx_0,ky_0,kz_0),\,k\neq 0\) is a solution too. So with a rational solution, an integer solution can be generated with ease (by letting \(k\) equals to least common multiple of denominators of \(x_0,y_0,z_0\)). This property also implies that one can assume \(z=1\), without losing any wanted solution.
Then the equation is reduced to a simpler one (with fewer variables):
\(x^3-3 x^2 y-3 x^2-3 x y^2-5 x y-3 x+y^3-3 y^2-3 y+1=0,\quad x,y\in\mathbb{Q}^{+{}}\)
But one can make it even simpler, by doing some (rational) linear transformation:
\[(X,Y,Z)^T=\left(\begin{array}{ccc} -\frac{95}{2} & -\frac{95}{2} & \frac{277}{12} \\ -\frac{91}{2} & \frac{91}{2} & 0 \\ -6 & -6 & 1 \\\end{array}\right) (x,y,z)^T\]
It is easy to verify that:
\[X^3-\frac{11209}{48}X Z^2+\frac{1185157}{864}Z^3-Y^2 Z=8281(x^3 + y^3 + z^3 - 3x^2(y+z) - 3y^2(z+x) - 3z^2(x+y) - 5xyz)\]
The new equation is \(x^3-\frac{11209}{48}x z^2+\frac{1185157}{864}z^3-y^2 z=0\). Since the transformation matrix is invertible (determinant is not zero), one can convert the solution of the new equation to the solution of the previous equation, without losing any potential solutions of the original equation.
Assuming \(z=1\), the equation can be reduced to \(x^3-\frac{11209}{48}x+\frac{1185157}{864}-y^2=0\). This type of equations (\(y^{2}=x^{3}+px+q\)) are Weierstrass equations. Since the discriminant \(\Delta =-16(4p^{3}+27q^{2})\) is non-singular (which implies that the curve of this equation has no cusps, self-intersections, or isolated points), it is, in fact, an elliptic curve.
Open-source software Sagemath can convert a cubic curve to an elliptic curve automatically:
sage: R.<x,y,z> = QQ[]; sage: F = x^3 + y^3 + z^3 - 3*x^2*(y+z) - 3*y^2*(z+x) - 3*z^2*(x+y) - 5*x*y*z; sage: WeierstrassForm(F) (-11209/48, 1185157/864)
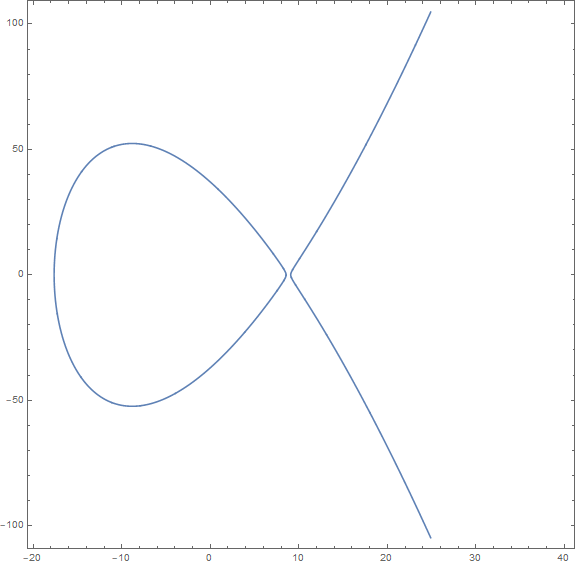
Each integer solution (with the greatest common divisor \(1\)) of the original equation one-to-one corresponds to a rational point on the elliptic curve, so finding integer solutions is equivalent to finding rational points on the curve.
But not all rational points correspond to a positive integer solution. Only rational points in the red region correspond to a positive integer solution. There are two parts of the red region: the left part has three intersections with the curve, while the right part has none.
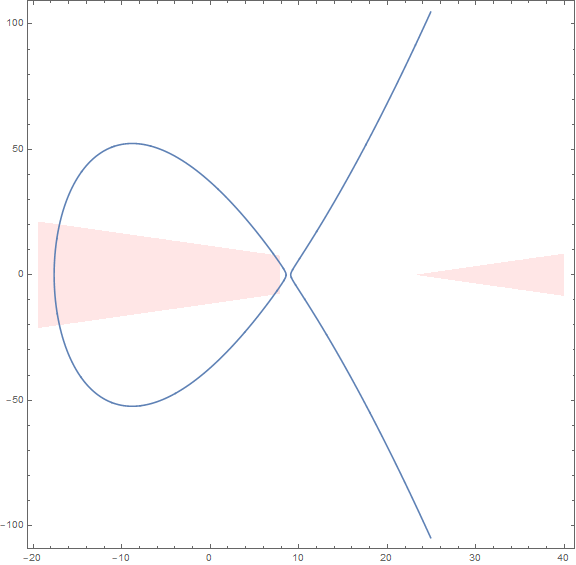
It is easy to verify that point \((x,y)\) on the curve lies in red region if and only if \(x\in(\frac{-39 \sqrt{65}-109}{24},\frac{-84 \sqrt{3}-59}{12})\cup(\frac{84 \sqrt{3}-59}{12},\frac{95}{12})\). One can write code to judge whether a point corresponds to a positive solution.
from sympy import sqrt O = ("Inf", "Inf") def is_valid(P): if P == O: return False else: return ((-39 * sqrt(65) - 109) / 24 < P[0] < (-84 * sqrt(3) - 59) / 12) or ( (84 * sqrt(3) - 59) / 12 < P[0] < 95 / 12)
After converting ranges to decimal form, one will get \(x\in(-17.64,-17.04)\cup(7.21,7.92)\), which is a small range. It is intuitive that there is little probability that a rational point locates in this range, thus finding a positive integer solution may be much harder than finding an integer solution.
4 Algebraic properties of elliptic curve
In mathematics, an elliptic curve is a plane algebraic curve defined by an equation of the form \(y^{2}=x^{3}+px+q\), which is non-singular.
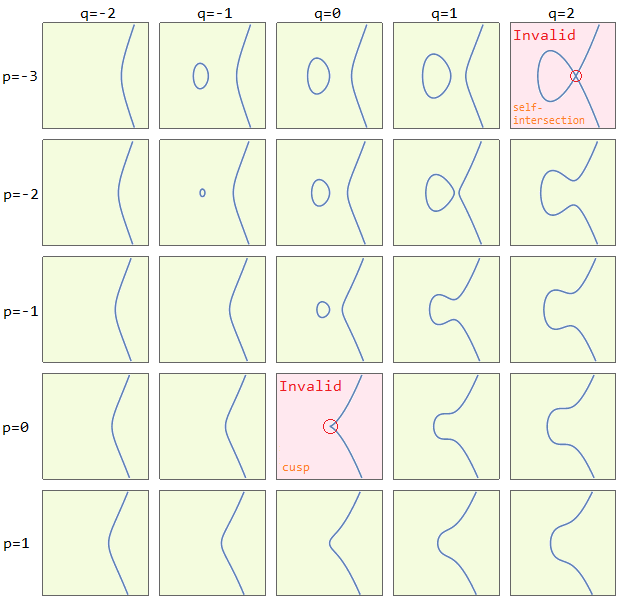
Since the curve is symmetrical about the x-axis, given any point \(P\), one can take \(-P\) to be the point opposite it. Define operation \(+\) on points: assume \(P, Q\) are two different points on the curve, draw the line that intersects \(P, Q\), which will generally intersect the cubic curve (uniquely) at a third point \(R\). Take \(P+Q\) to be \(-R\), the point opposite \(R\).
- Situation 1 (generally):
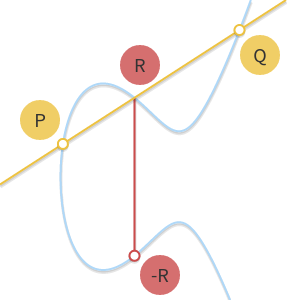
A curve will have an additional point at infinity, \(O\). Taking \(-O\) to be just \(O\), \(P+(-P)=O,\,O+P=P=P+O\) will hold for all points \(P\). (\(O\) on elliptic curve serves like zero in integer addition arithmetic)
There are some other special situations:
- Situation 2 (\(P=Q\)):
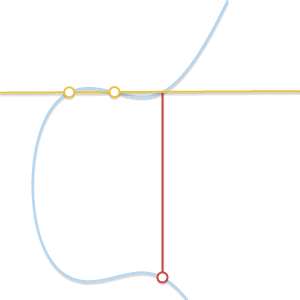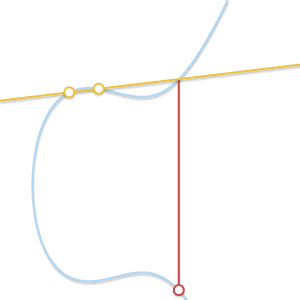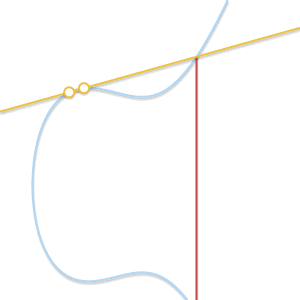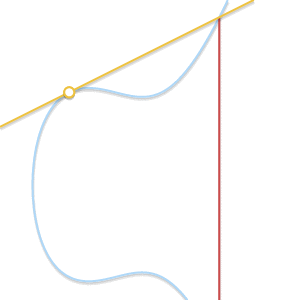
- Situation 3 (the line is a tangent line at point \(P\) or \(Q\)):
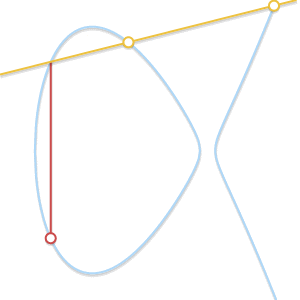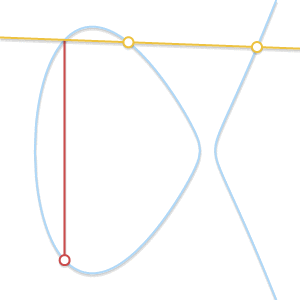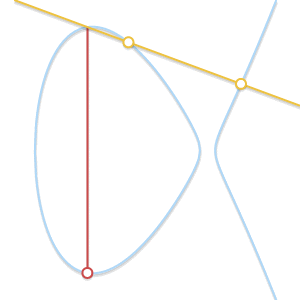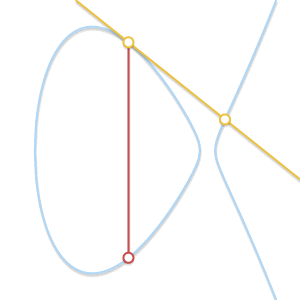
(Images of various situations above come from Andrea Corbellini's blog)
The reader can change values of \(p,q\), and move points \(P,Q\), to visualize addition operation on an elliptic curve. (you can also zoom, full screen, move, reset canvas)
Addition of points on elliptic curve can be defined not only geometrically, but also algebraically, which is more precise. Given the curve \(y^2 = x^3 + px + q\) over the field \(K\) whose characteristic is assumed to be neither \(2\) nor \(3\), and points \(P = (x_P, y_P)\) and \(Q = (x_Q, y_Q)\) on the curve. Let \(s\) be the slope of the line containing \(P\) and \(Q\); i.e., \(s={\frac {y_{P}-y_{Q}}{x_{P}-x_{Q}}}\).
- \({\displaystyle x_P\neq x_Q}\): \({\displaystyle x_R=s^2-x_P-x_Q,\,y_R=-y_P+s(x_P-x_R)}\)
- \({\displaystyle x_P=x_Q}\):
- \({\displaystyle y_P=-y_Q}\): \({\displaystyle P+Q=O}\)
- \({\displaystyle y_P=y_Q}\): \({\displaystyle R=2P,\,s=\frac{3x_P^2+p}{2y_P},\,x_R=s^2-2x_P,\,y_R=-y_P+s(x_P-x_R)}\)
Code for doing points addition:
from fractions import Fraction as Frac O = ("Inf", "Inf") def ec_plus(P, Q): if P == O: return Q if Q == O: return P R = [None] * 2 if P[0] == Q[0]: if P[1] == -Q[1]: R = O else: s = (3 * P[0]**2 + -Frac(11209, 48)) / (2 * P[1]) R[0] = s**2 - 2 * P[0] R[1] = -P[1] + s * (P[0] - R[0]) else: s = (P[1] - Q[1]) / (P[0] - Q[0]) R[0] = s**2 - P[0] - Q[0] R[1] = -P[1] + s * (P[0] - R[0]) return tuple(R)
It's easy to prove \(P,Q,-(P+Q)\) are collinear with algebraic definition. Points set \(G\) on elliptic curve (include \(O\)) satisfies following properties:
- Closure: For all \(P,Q\) in \(G\), the result of the operation \(P+Q\) is also in \(G\).
- Associativity: For all \(P,Q,R\) in \(G\), the equation \((P+Q)+R=P+(Q+R)\) holds.
- Identity element: There exists an element \(O\) in \(G\), such that for all elements \(P\) in \(G\), the equation \(O+P=P=P+O\) holds.
- Inverse element: For each \(P\) in \(G\), there exists an element \(Q\) in \(G\) such that \(P+Q=O=Q+P\), where \(O\) is the identity element.
- Commutativity: For all \(P,Q\) in \(G\), the equation \(P+Q=Q+P\) holds.
These properties show that points and additions on elliptic curve \((G,{}+)\) forms an abelian group (also called commutative group), and \(O\) is identity element. It is easy to verify that when taking all rational points (and \(O\)) from \(G\), the above five properties will still hold, which means that after finding a rational point \(P\), one can generate infinitely many rational points by calculating \(2P=P+P,\,3P=2P+P,\,\cdots\). It is far more efficient at finding rational points than brute-forcing approach.
Elliptic curves are familiar in cryptography, due to its abelian group property, just like RSA. However, a quantum computer can crack cryptosystems based on an abelian group efficiently.
5 Generating solutions
It is known that finding an integer solution (not necessary positive) is easy, therefore one can get several rational points on the curve by brute forcing integer solutions of original equation.
from fractions import Fraction as Frac from math import gcd n = 100 for x in range(-n, n + 1): for y in range(-n, n + 1): for z in range(0, n + 1): if gcd(x, gcd(y, z)) == 1: if x**3 + y**3 + z**3 - 3 * x**2 * (y + z) - 3 * y**2 * ( z + x) - 3 * z**2 * (x + y) - 5 * x * y * z == 0: print((x, y, z))
(-11, -9, 5) (-11, -4, 1) (-9, -11, 5) (-5, 9, 11) (-5, 11, 9) (-4, -11, 1) (-1, -1, 1) (-1, 0, 1) (-1, 1, 0) (-1, 1, 1) (-1, 4, 11) (-1, 11, 4) (0, -1, 1) (1, -1, 0) (1, -1, 1) (4, -1, 11) (9, -5, 11) (11, -5, 9) (11, -1, 4)
Pick (-1, 4, 11) as an example, transform it with the matrix:
\[\left(\begin{array}{ccc} -\frac{95}{2} & -\frac{95}{2} & \frac{277}{12} \\ -\frac{91}{2} & \frac{91}{2} & 0 \\ -6 & -6 & 1 \\\end{array}\right) (-1,4,11)^T = (\frac{1337}{12},-\frac{455}{2},-7)^T = -7\cdot(-\frac{191}{12},\frac{65}{2},1)^T\]
This solution corresponds to point \(P=(-\frac{191}{12},\frac{65}{2})\).
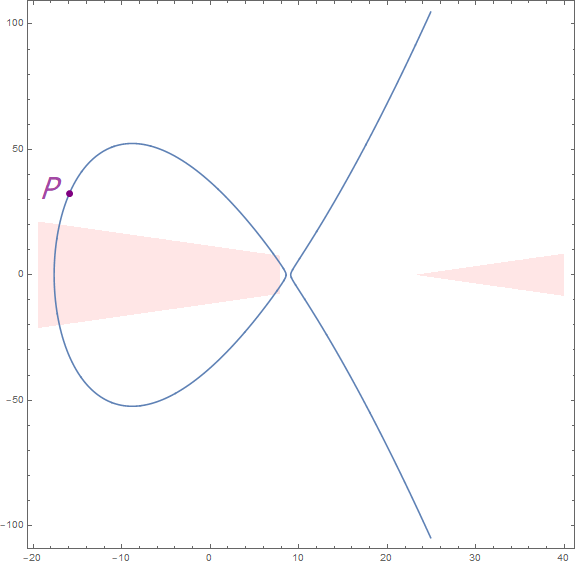
This point lies outside the red region. However, do not worry, one can use point addition to get a lot of rational points (with code below) until a valid point occurs.
<<is_valid>> <<ec_plus>> P = S = (-Frac(191, 12), Frac(65, 2)) cnt = 1 while not is_valid(S): S = ec_plus(S, P) cnt += 1 print("{}P = ({}, {})".format(cnt, *S))
2P = (29233/300, -237679/250) 3P = (-449023/71286, 263764935/5180116) 4P = (2595564718153/100280426700, -171959440568022731/1527855867796750) 5P = (378326742585987529/182304915530542572, 112103221774745790541183075/3745033395604274176822442) 6P = (733306806381056483585521/52901390736340463822400, -343764653760831645784970282294394569/12167479807190947672003083538368000) 7P = (12186898088049137933023410813097849/1960207391964596384635579845637932, 52847537824372995383455949500060960584963350540405/4175525694290461543876101536662682824637424706682) 8P = (184291903459371594568624235201241521313551833/17546136990312774398727858490642680612252300, -31167188094052845691703198380025832449772385839996621463599210371/3536147729595630697250285084695028312237650433064461603785465250) 9P = (637231263346693346010600868176842100660564986054619857/81086401756297731072425447670017660116155468002441526, 29400417578654041653688375863673590665042836425148365175935874356653994350305605/6284274674391913738225458829167585075352347781720125288787017561681121629385876)
The results above show that the denominators of coordinates of rational points are overgrowing.
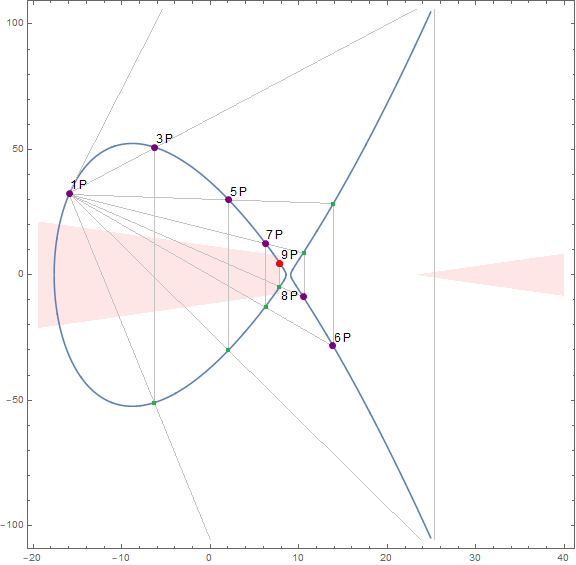
Use inverse of original transformation matrix to transform \(9P\) back to correspond rational solution:
\[\left(\begin{array}{ccc} \frac{1}{182} & -\frac{1}{91} & -\frac{277}{2184} \\ \frac{1}{182} & \frac{1}{91} & -\frac{277}{2184} \\ \frac{6}{91} & 0 & -\frac{95}{182} \\\end{array}\right) \left(\begin{array}{c} x_{9P} \\ y_{9P} \\ 1\\\end{array}\right) = \left(\begin{array}{c} -\frac{36875131794129999827197811565225474825492979968971970996283137471637224634055579}{1143737990739328300357033506908500483714127296273062802559237196225964136548229432} \\ -\frac{154476802108746166441951315019919837485664325669565431700026634898253202035277999}{1143737990739328300357033506908500483714127296273062802559237196225964136548229432} \\ -\frac{9405501114660716625534518421595417184664937929417781}{2459620853274364509196905245990535690190049196074059622}\\\end{array}\right)\]
Then, by multiplying the lowest common multiple of denominators and taking the opposite number, one will finally get the positive integer solution!
x = 36875131794129999827197811565225474825492979968971970996283137471637224634055579 y = 154476802108746166441951315019919837485664325669565431700026634898253202035277999 z = 4373612677928697257861252602371390152816537558161613618621437993378423467772036
6 Some interesting facts
You may be wondering how to prove that this positive integer solution is the smallest one. If so, you will be interested in following facts.
6.1 Will digits of denominators of \(nP\) keep growing?
It will keep growing, proportional to \(n^2\), but that is not easy to prove, since there is always a possibility of some cancellation. For this reason, mathematicians defined Canonical height of a point as \(\hat h_L(P) = \lim_{N\rightarrow\infty}\frac{h_L(NP)}{N^2}\) where \(h_L(\frac{p}{q})=\log\max(\lvert p\rvert,\lvert q\rvert),\,p\bot q\), which has a lot of properties.
6.2 If there exists a rational point \(Q\) and positive integer \(n\) that satisfies \(nQ=O\)?
For example, point \(Q=(\frac{277}{12},-91)\) corresponds to solution (1, -1, 1) satisfies \(6Q=O\).
<<ec_plus>> Q = (Frac(277, 12), -Frac(91)) S = O for cnt in range(1, 8): S = ec_plus(S, Q) print("{}Q = ({}, {})".format(cnt, *S))
1Q = (277/12, -91) 2Q = (121/12, -13/2) 3Q = (109/12, 0) 4Q = (121/12, 13/2) 5Q = (277/12, 91) 6Q = (Inf, Inf) 7Q = (277/12, -91)
In fact, on this elliptic curve, only points \(O,1Q,2Q,3Q,4Q,5Q\) have such property. Points that have such properties are torsion points. They have Canonical height \(0\) and formed the torsion subgroup of the original abelian group.
Mazur provided a complete list of possible torsion subgroups for rational elliptic curves:
- \(\mathbb Z/ N\mathbb Z,\quad N = 1, 2, \dots, 10, 12\)
- \(\mathbb Z/2\mathbb Z \times \mathbb Z/2N\mathbb Z,\quad N = 1, 2, 3, 4\)
Sagemath can find all points that form a torsion subgroup on an elliptic curve.
sage: E = EllipticCurve([-11209/48, 1185157/864]) sage: E.torsion_subgroup() Torsion Subgroup isomorphic to Z/6 associated to the Elliptic Curve defined by y^2 = x^3 - 11209/48*x + 1185157/864 over Rational Field sage: E.torsion_points() [(0 : 1 : 0), (109/12 : 0 : 1), (121/12 : -13/2 : 1), (121/12 : 13/2 : 1), (277/12 : -91 : 1), (277/12 : 91 : 1)]
Torsion points are straightforward to find, due to the Nagell-Lutz theorem.
6.3 Can all rational points generated using additions from several points?
The Mordell-Weil theorem states that for an abelian variety \(A\) over a number field \(K\), the group \(A(K)\) of K-rational points of \(A\) is a finitely generated abelian group, called the Mordell-Weil group. In this case, \(A\) is an elliptic curve, and \(K\) is the rational number field \(Q\). So the abelian group of rational points on an elliptic curve has the form \(T \times Z^r\) , where \(T\) is the torsion subgroup, and \(r\) is the rank of the elliptic curve. That means torsion points together with \(r\) generators can generate all rational points of an elliptic curve, using addition operations only.
One can get the rank of an elliptic curve as well as all generators with Sagemath. When Sagemath cannot calculate precise rank, one can calculate bounds of rank instead.
sage: E = EllipticCurve([-11209/48, 1185157/864]) sage: E.rank() 1 sage: E.gens() [(-191/12 : 65/2 : 1)] sage: E.rank_bounds() (1, 1)
A common conjecture is that there is no bound on the largest possible rank for an elliptic curve. Scientists have discovered an elliptic curve with a rank of at least 28 and an elliptic curve with a rank of precisely 19.
Thanks to the beautiful algebraic properties of the curve and the power of mathematics, one can find generators much faster than brute-forcing. With logic, one can eliminate lots of possibilities in a heartbeat.
6.4 What if generalizing the equation to \(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}=n\)?
Intersection range of elliptic curve and red region will become smaller as \(n\) grows. So finding a rational point inside the red region will expect more iterations, leading to larger solutions.
When \(n\) is odd, the equation always has no solution. Rational points will always locate on the right part of the elliptic curve, never corresponding to a positive integer solution.
When \(n\) is even, the equation sometimes has solutions. Maximum number of digits in \(x,y,z\) of minimal solutions are given in the following table. \(m\) means the solution corresponds to point \(mp+t\) where \(p\) is a generator and \(t\) is a torsion point.
| n | m | #digits | n | m | #digits | n | m | #digits |
| 4 | 9 | 81 | 48 | 311 | 418086 | 136 | 65 | 26942 |
| 6 | 11 | 134 | 58 | 221 | 244860 | 146 | 307 | 259164 |
| 10 | 13 | 190 | 60 | 61 | 9188 | 156 | 353 | 12046628 |
| 12 | 35 | 2707 | 66 | 107 | 215532 | 158 | 1211 | 15097279 |
| 14 | 47 | 1876 | 76 | 65 | 23662 | 162 | 457 | 1265063 |
| 16 | 11 | 414 | 82 | 157 | 85465 | 178 | 2945 | 398605460 |
| 18 | 49 | 10323 | 92 | 321 | 252817 | 182 | 853 | 2828781 |
| 24 | 107 | 33644 | 102 | 423 | 625533 | 184 | 851 | 20770896 |
| 28 | 121 | 81853 | 112 | 223 | 935970 | 186 | 643 | 5442988 |
| 32 | 65 | 14836 | 116 | 101 | 112519 | 196 | 701 | 11323026 |
| 38 | 659 | 1584369 | 126 | 75 | 196670 | 198 | 121 | 726373 |
| 42 | 419 | 886344 | 130 | 707 | 8572242 | 200 | 2957 | 71225279 |
| 46 | 201 | 198771 | 132 | 461 | 3607937 |
The size of the smallest solution of this equation grows very fast as \(n\) grows.
7 Go a step further
What an awesome equation! However, one may be wondering a harder equation. So it comes to degree-4 Diophantine equations.
It seems that it is an endless effort, for one can always increase the degree of an equation to make it harder. However, degree-4 is hard enough, since Mathematicians have found a degree-4 Diophantine equation (with \(58\) variables, and some of them are parameters) that is universal.
That means, one can reduce any Diophantine equation to a degree-4 Diophantine equation, and there does not exist an algorithm that can determine whether this equation has a solution (given values of parameters). As a result, mathematics cannot do that too. We finally reached the limit of computation and mathematics!
This step is not an ordinary step, but a step towards the abyss of unknowns. It is related to Hilbert's tenth problem. The author will post an article on this later. (On Hilbert's tenth problem)
8 References
- An unusual cubic representation problem Andrew Bremner, Allan Macleod
- https://en.wikipedia.org/wiki/Elliptic_curve Elliptic curve - Wikipedia